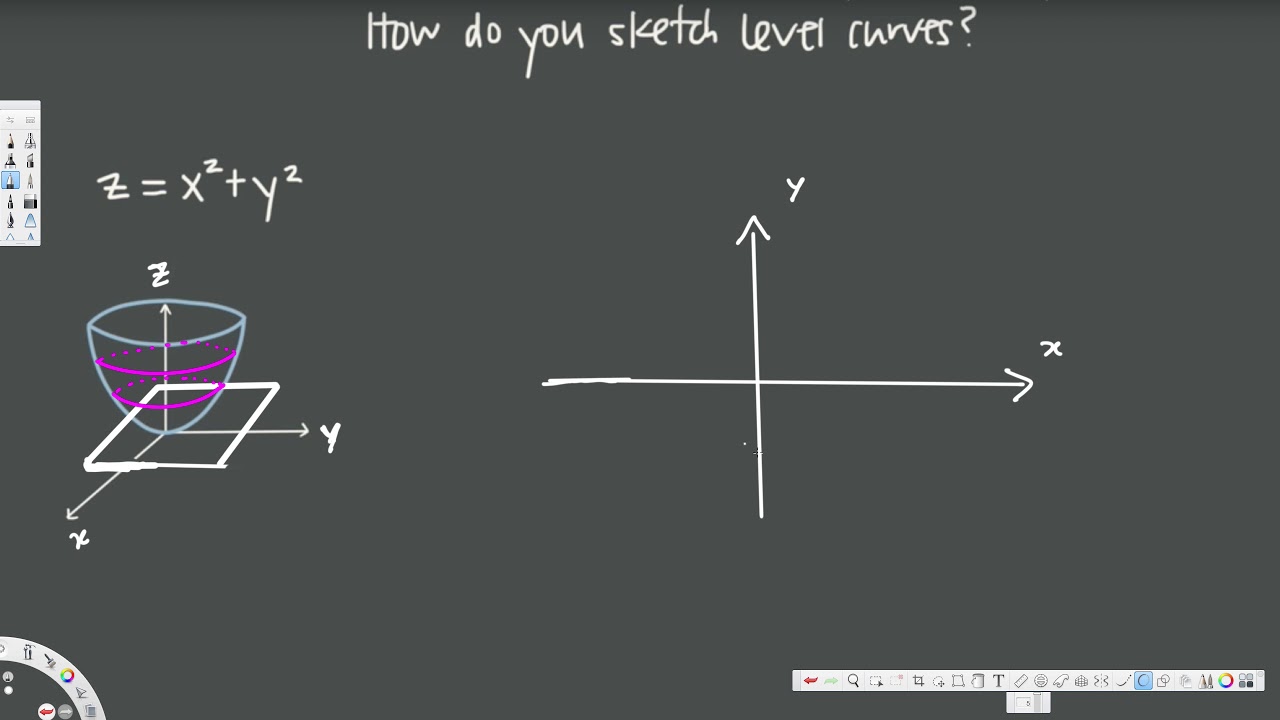
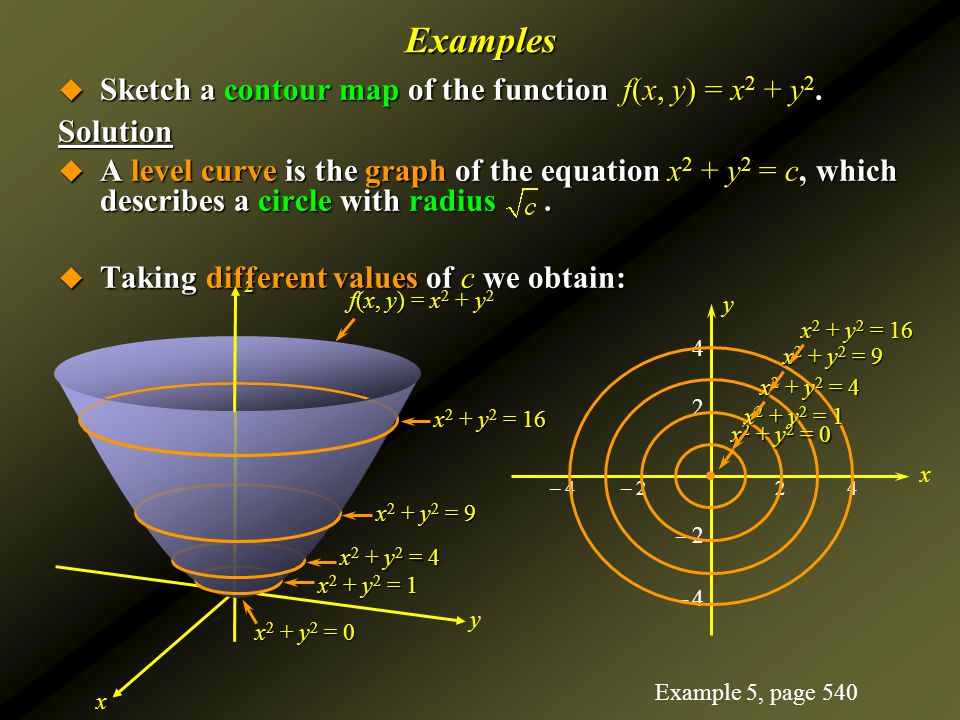
So level curves, level curves for the function z equals x squared plus y squared, these are just circles in the xyplane And if we're being careful and if we take the convention that our level curves are evenly spaced in the zplane, then these are going to get closer and closer together, and we'll see in a minute where that's coming fromLevel curves, contour curves Definition The level curves of a function f D ⊂ R2 → R ⊂ R are the curves in the domain D ⊂ R2 of f solutions of the equation f (x,y) = k, where k ∈ R is a constant in the range of f The contour curves of function f are the curves in R3 given by theDescribe the level curves of the function Sketch the level curves for the given c values z=62 x3 y, \quad c=0,2,4,6,8,10 Get certified as an expert in
1
Level curves of a continuous function
Level curves of a continuous function- What we want to be able to do is slice through the figure at all different heights in order to get what we call the "level curves" of a function Then we want to be able to transfer all those twodimensional curves into the twodimensional plane, sketching those in the xyplane This will give us the sketch of level curves of the function1 Level Surfaces 2 If one of the Arguments is time we can animate ie w = f(x,y,t) Level Surfaces Given w = f(x,y,z) then a level surface is obtained by considering w = c = f(x,y,z) The interpretation being that on a level surface f has the same value at every pt For example f could represent the temperature at each pt in 3space




Graphs And Level Curves
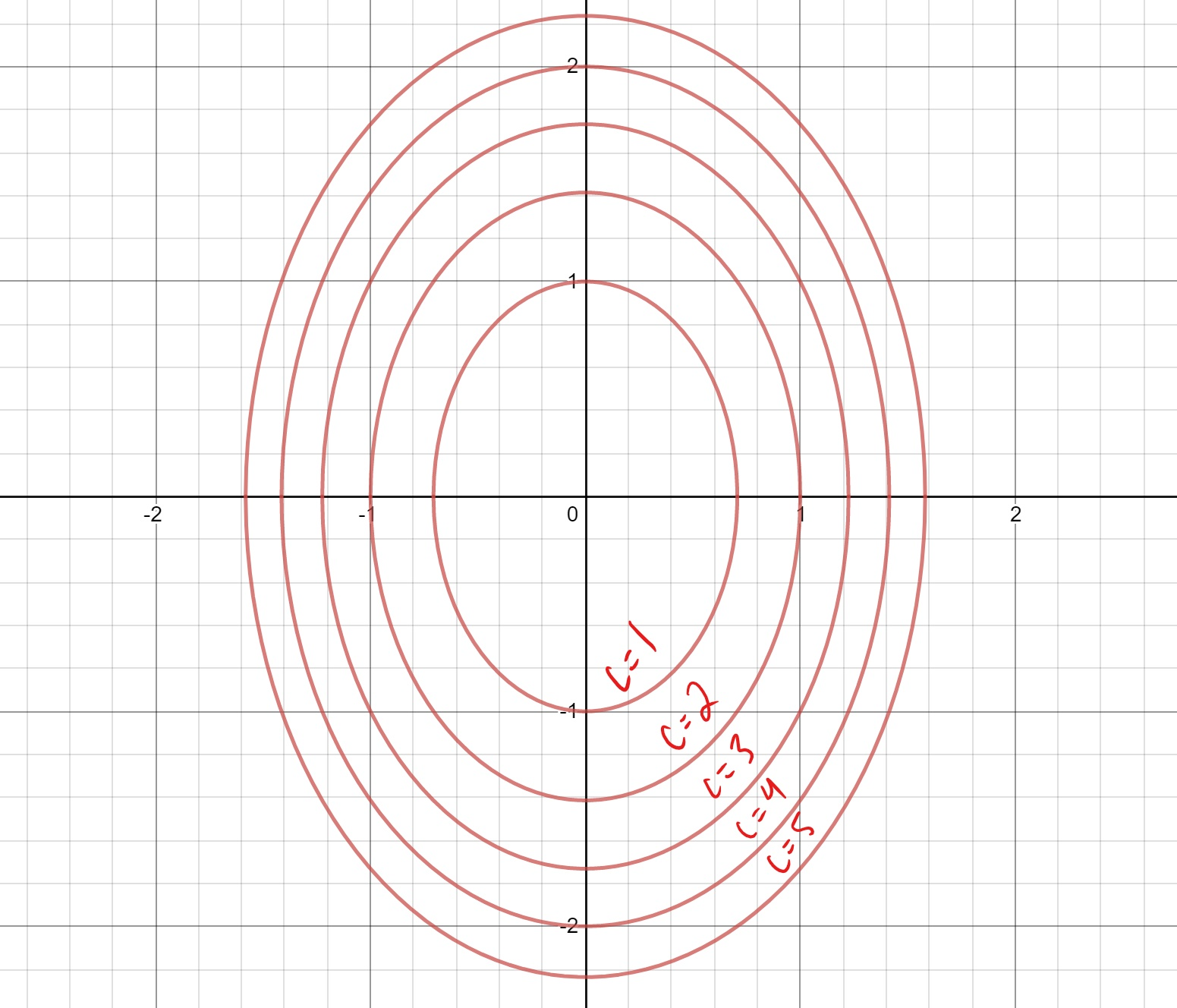
Level Curves Author Kristen Beck Topic Functions This worksheet illustrates the level curves of a function of two variables You may enter any function which is a polynomial in both and By letting Z equal to some constant 'c' we get a single level curve I would like to obtain an expression of the resulting function of the form y=f(x) to be able to study other properties of it Basic Example 1 Easy game Let's consider the problem of plotting level curves of z=x^2y^2100 for x,y10;10 and z=1 A level curve of a function f (x,y) is a set of points (x,y) in the plane such that f (x,y)=c for a fixed value c Example 5 The level curves of f (x,y) = x 2 y 2 are curves of the form x 2 y 2 =c for different choices of c These are circles of radius square root of c
More We want to sketch the following level curves For the function F Of X Y is equal to two X plus three Y Okay The equals negative two negative 101 and two This question is testing our basic abilities to work with functions of multiple variables Which is essential for moving forward in multi variable calculus The level curves of the function z = f (x,y) z = f (x, y) are two dimensional curves we get by setting z = k z = k, where k k is any number So the equations of the level curves are fMatlab simpli es the process of constructing level curves, even for the most di cult of functions Example 1 Sketch several level curves of the function f R2!R de ned by f(x;y)= −3y x2 y2 1 (3) over the region f(x;y)−2 x 2;−2 y 2gand label each level curve with its constant function value Solution First use the meshgrid command to
There is a close relationship between level curves (also called contour curves or isolines) and the gradient vectors of a curve Indeed, the two are everywhere perpendicular This handout is going to explore the relationship between isolines and gradients to help us understand the shape of functions in three dimensions This is a common application in physics when considering lines ofLevel Curve Grapher Level Curve Grapher Enter a function f (x,y) Enter a value of c Enter a value of c Enter a value of c Enter a value of cGet the free "Level Curves" widget for your website, blog, Wordpress, Blogger, or iGoogle Find more Mathematics widgets in WolframAlpha



Level Curves Physics Forums




Mcmaster University Math Test 1m03 12 Level Curves Of Function Topic Play
LEVEL CURVES OF HARMONIC FUNCTIONS 85 2 Curvature In this section, we investigate the curvature κ of Z ⊂ R2, when u is harmonic Jerrard and Rubel 5provedthatlogκ is superharmonic, on a nice enough domain See 8 for another monotonicity property of curvature Unfortunately, these do not seem to say much about a given level curveLevel Curves In mathematics, a level set of a realvalued function f of n real variables is a set where the function takes on a given constant value cRelief Functions and Level Curves Purpose The purpose of this lab is to introduce you to plots of relief functions and level curves on surfaces Several Maple procedures will be introduced to help with visualization Background In this lab we will consider the case of a surface defined explicitly by an equation of the form z = f(x, y)



Level Sets Math Insight




Lesson 15 Gradients And Level Curves
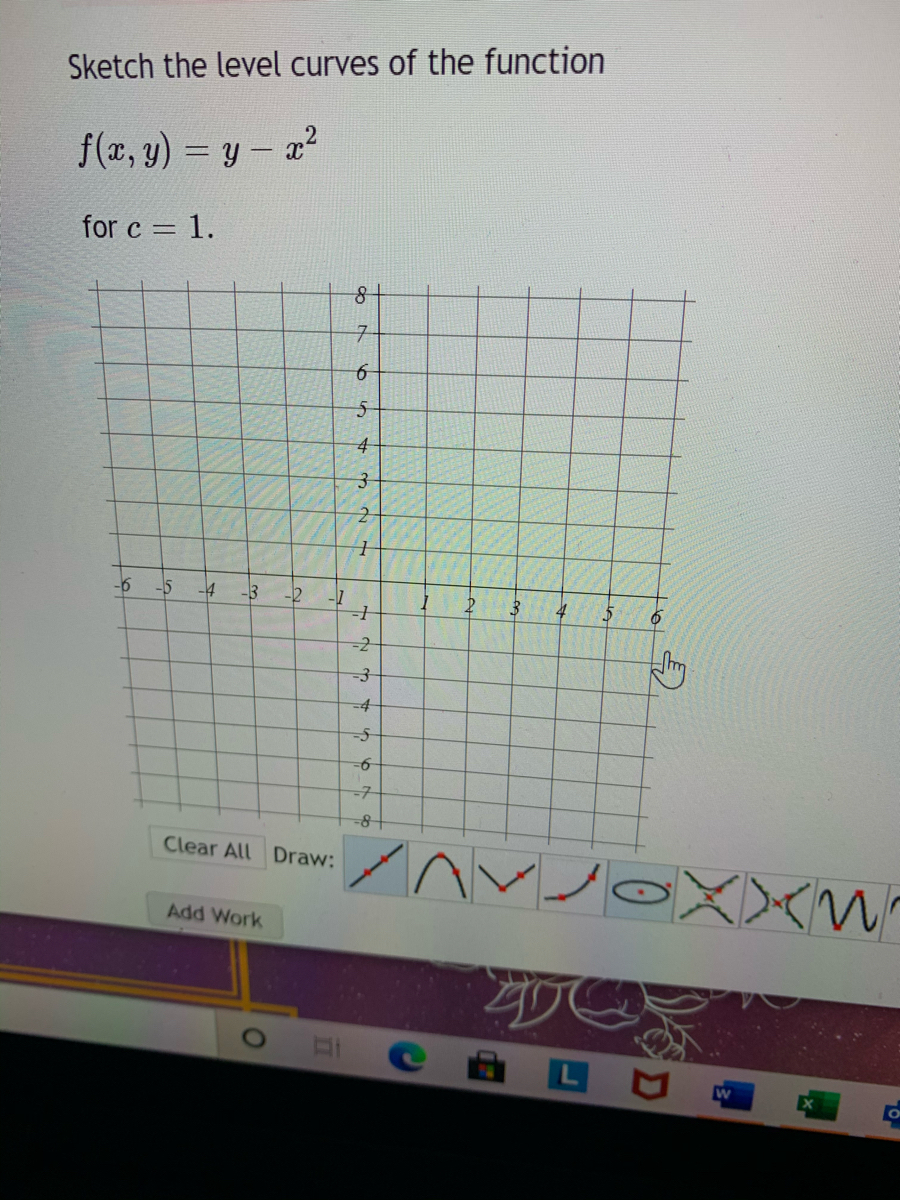
Consider the function f (x, y) = (x − 1) 2 y e x 3 y Setting it equal to zero, we get x = 1 or y = 0 According to my understanding, these two lines should be the level curves However, if I plot the function using a 3D plotter (GeoGebra in my case), it only seems to show y = 0 as the level curve (the black line in the figure)Describe the level curves of the function z = 6 − 2x − 3y Sketch a contour map of the surface using level curves for the given cvalues c = 0, 2, 4, 6, 8, 10The level curve of this function for the value 2 is empty (there are no values of (x, y) such that f(x, y) = 2) and the level curve for the value 1 is the set all all points (x, y) In less extreme examples, some but not all level curves are sets



Www Usna Edu Users Math Uhan Sm223 Lessons 12 level curves Pdf




Calculus 11 1 Functions Of Several Variables Flashcards Quizlet
Figures ()(VI) show level curves of six functions around a critical point P Does each function have a local maximum, a local minimum, or a saddle point at P?Select a function from the dropdown menu or type your own function in the text box below and click "Enter" to plot it Click the radio buttons to view either a level curve or a cross section Use the slider to change the value of the related constant k, c, or d Click "Reset" to reset both plots Calculus questions and answers 6 Find the equations of level curves of the function z= =f (x, y) = 369x² 4y2 , and sketch the graphs of these level curves 7 Use implicit differentiation to find Oz дх дz and if x² y2 z² – 2xyz = 5 Question 6



Http Math Oregonstate Edu Garity 254h Winter13 Notes 10 Graphs Levelcurves Pdf




Level Sets Ximera
The whole point of a "level" curve is that the function stays at the same "level", ie the same value The level curve is f(x,y)= yx 2 y 2 = 3 Yes, your tangent line is correct A level curve of a function f(x,y) is the curve of points (x,y) where f(x,y) is some constant value A level curve is simply a cross section of the graph of z=f(x,y) taken at a constant value, say z=c A function has many level curves, as one obtains a different level curve for each value of c in the range of f(x,y)Level curves The two main ways to visualize functions of two variables is via graphs and level curves Both were introduced in an earlier learning module Level curves for a function z = f ( x, y) D ⊆ R 2 → R the level curve of value c is the curve C in D ⊆ R 2 on which f C = c Notice the critical difference between a level curve C




Graphs And Level Curves
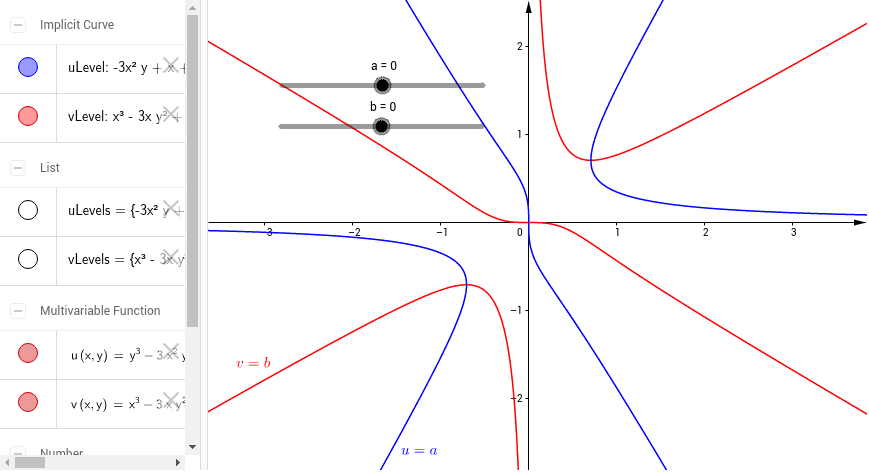



Level Curves Geogebra
Level Curves and Surfaces The graph of a function of two variables is a surface in space Pieces of graphs can be plotted with Maple using the command plot3dFor example, to plot the portion of the graph of the function f(x,y)=x 2 y 2 corresponding to x between 2 and 2 and y between 2 and 2, type > with (plots); How to Find the Level Curves of a Function Calculus 3 How to Find the Level Curves of a Function Calculus 3Gradients, Normals, Level Curves Objectives In this lab you will demonstrate the relationship between the gradients and level curves of functions The Gradient as a Vector Operator The gradient of a function, is a vector whose components are the partials of the original function;




Contour Maps In Matlab
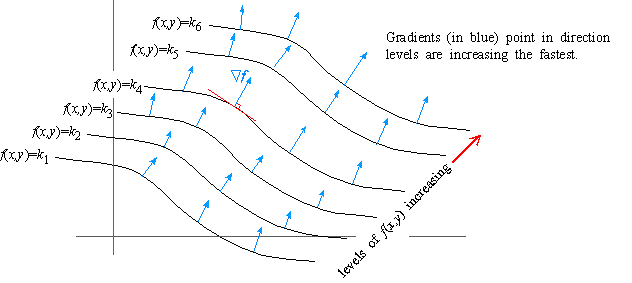



Gradients And Level Curves
Level surfaces For a function $w=f(x,\,y,\,z) \, U \,\subseteq\, {\mathbb R}^3 \to {\mathbb R}$ the level surface of value $c$ is the surface $S$ in $U \subseteqThen the curves obtained by the intersections of the planes, with the graph of are called the Level Curves of From the definition of a level curve above, we see that a level curve is simply a curve of intersection between any plane parallel to the axis and the surface generated by the functionLevel Curves Def If f is a function of two variables with domain D, then the graph of f is {(x,y,z) ∈ R3 z = f(x,y) } for (x,y) ∈ D Def The level curves of a function f(x,y)are the curves in the plane with equations f(x,y)= kwhere is a constant in the range of f The contour curves are the corresponding curves on the surface, the




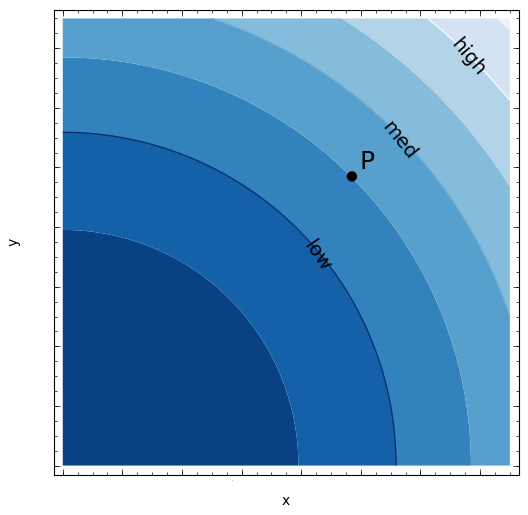
The Figure Shows Level Curves Of A Function F X Y A Draw Gradient Vectors At Q And T Is Nabla F Q Longer Than Shorter Than Or The Same Length As Nabla F T



1
If I want the level curves f ( x, y) = c, then these now represent concentric circles in the x − y plane centered at the origin of radius c Now here's my question Say I have w = f ( x, y, z) now a function of three variables, ie it is a hypersurface in R 4 If I have a level "curve" say w = f ( x, y, z) = 0, does this then represent now aDefinition The level curves of a function f of two variables are the curves with equations f (x,y) = k, where k is a constant (in the range of f) A level curve f (x,y) = k is the set of all points in the domain of f at which f takes on a given value k In other words, it shows where the graph of f has height kLevel Curves and Contour Plots Level curves and contour plots are another way of visualizing functions of two variables If you have seen a topographic map then you have seen a contour plot Example To illustrate this we first draw the graph of z = x2 y2 On this graph we draw contours, which are curves at a fixed height z = constant




Graphs And Level Curves



Www Math Uci Edu Remote Teaching Lecture Notes Of Hamed Math 2d lecture notes Lecture note 14 1 Pdf
Level sets show up in many applications, often under different names For example, an implicit curve is a level curve, which is considered independently of its neighbor curves, emphasizing that such a curve is defined by an implicit equationAnalogously, a level surface is sometimes called an implicit surface or an isosurface The name isocontour is also used, which means a contour ofA level curve of a function f (x, y) is the curve of points (x, y) where f (x, y) is some constant value A level curve is simply a cross section of the graph of z = f (x, y) taken at a constant value, say z = c A function has many level curves, as one obtains a different level curve for each value of c in the range of f (x, y)A level curve can be drawn for function of two variable ,for function of three variable we have level surface A level curve of a function is curve of points where function have constant values,level curve is simply a cross section of graph of f




Univ Vector Calculus Drawing A Contour Map With Level Curves Learnmath



1
Returning to the function \(g(x,y)=\sqrt{9−x^2−y^2}\), we can determine the level curves of this function The range of \(g\) is the closed interval \(0,3\) First, we choose any number in this closed interval—say, \(c=2\) The level curve corresponding to \(c=2\) is described by the equation \ \sqrt{9−x^2−y^2}=2\The level curves are in the range of the function The level curves are on the surface The level curves can also be thought of as the intersection of the plane with the surface We often mark the function value on the corresponding level set If we choose function values which have a constant difference, then level curves are close togetherCurves in R2 Graphs vs Level Sets Graphs (y= f(x)) The graph of f R !R is f(x;y) 2R2 jy= f(x)g Example When we say \the curve y= x2," we really mean \The graph of the function f(x) = x2"That is, we mean the set f(x;y) 2R2 jy= x2g Level Sets (F(x;y) = c) The level set of F R2!R at height cis f(x;y) 2R2 jF(x;y) = cg Example When we say \the curve x 2 y = 1," we really mean




1 Sketch A Few Of The Level Curves Of The Function F X Y Surface Z Homeworklib




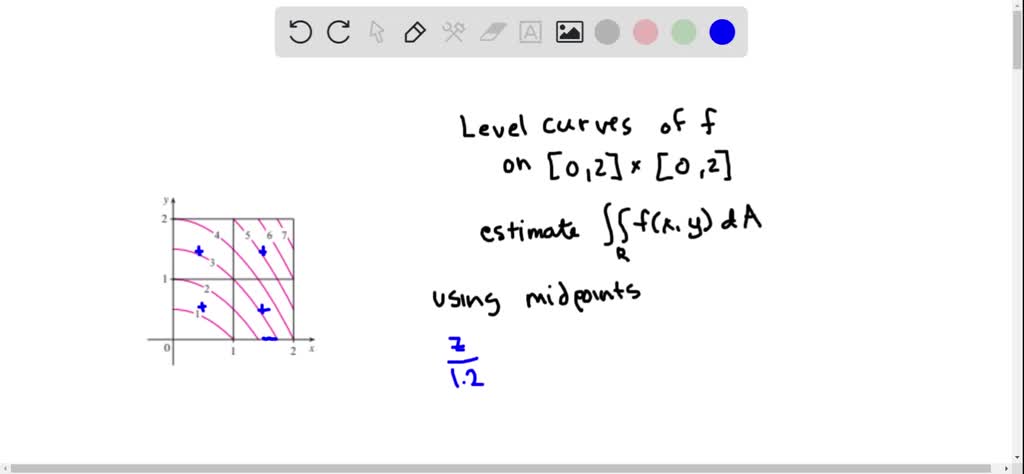
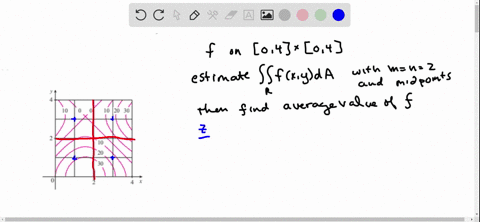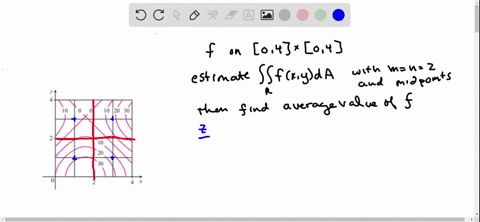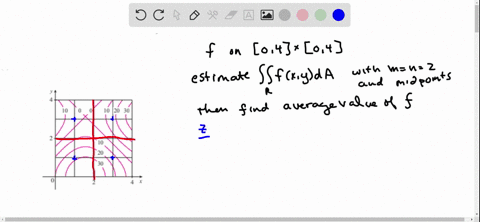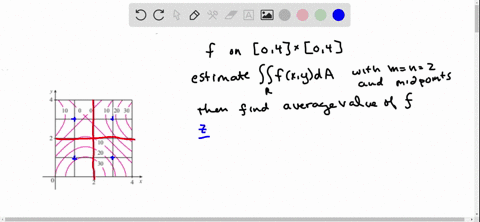
The Figure Shows Level Curves Of A Function F In The Square R 0 6 Times 0 6 Use The Midpoint Rule With M N 2 To Estimate
3 2 2 0 2 3Given a function z = f (x, y), we can draw a "topographical map" of f by drawing level curves (or, contour lines) A level curve at z = c is a curve in the x y plane such that for all points ( x , y ) on the curve, f ( x , y ) = cTwoDimensional Calculus (11) Chapter 2 Differentiation 8 Level curves and the implicit function theorem Let f(x, y) be continuously differentiable in a domain D and let (x 0, y 0) be any point in DThe equation f(x, y) = f(x 0, y 0) defines a level curve through the point (x 0, y 0)Let us assume for the moment that this level curve is the implicit form of a regular curve C, at least




Pdf Notes On The Level Curves Of A Meromorphic Function Semantic Scholar



Draw Level Curves For Functions Of Two Variables In C C Helper
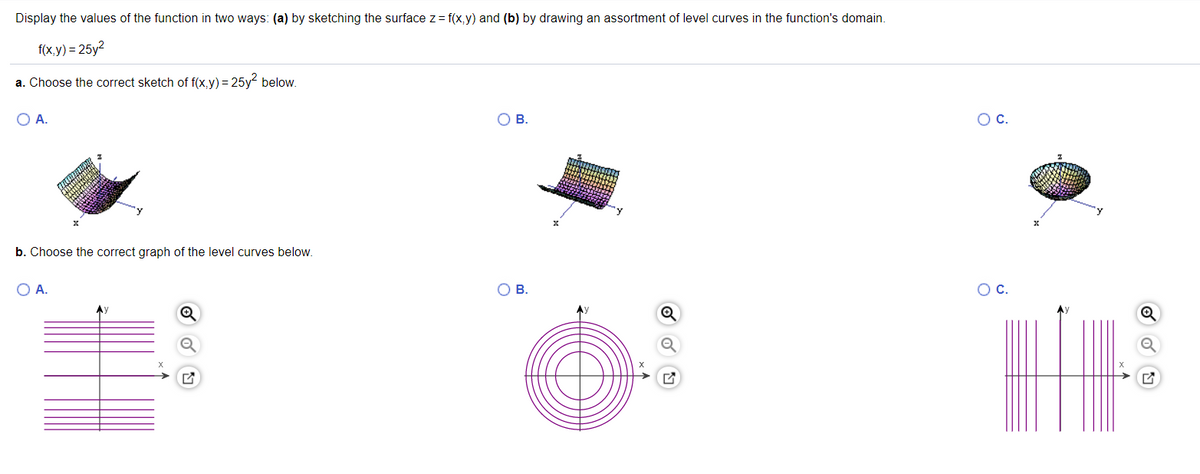
Define the function by fx_,y_ = (x^2 4 y^2) Exp1 x^2 y^2Level curves allow to visualize functions of two variables f(x,y) Example For f(x,y) = x2− y2 the set x2− y2= 0 is the union of the lines x = y and x = −y The set x2− y2= 1 consists of two hyperbola with with their "noses" at the point (−1,0) and (1,0)Level Curves So far we have two methods for visualizing functions arrow diagrams and graphs A third method, borrowed from mapmakers, is a contour map on which points of constant elevation are joined to form contour curves, or level curves A level curve f (x, y) = k is the set of all points in the domain of f at which f takes on a given value k




Level Curves Of Warga S Function F X 1 X 2 X 1 X 2 1 2 Download Scientific Diagram




Level Curves Of Functions Of Two Variables Youtube
Level Curves We are given a function two variables f(x,y) f (x, y) The level curves are represent the set of points in the xy plane where the function assumes a constant value For example, theNote that the gradient vectors are orthogonal to the level surface and point in the direction of maximum increase Matlab Files Although the following file features advanced use of Matlab, we include it here for those interested in discovering



Solved The Figure Shows Level Curves Of A Functio




Level Curves Of The Error Function Download Scientific Diagram



Describe The Level Curves Of The Function Sketch A Contour Map Of The Surface Using Level Curves For The Given C Values Z 2x Y C 1 2 3 4 5 Homework Help And Answers Slader




The Level Curves Of The Function U For The Condenser In Example 6 3 For Download Scientific Diagram




Level Surfaces




Help With Partial Derivatives On A Level Curve Calculus




28 36 38 40 41 15 1 Graphs And Level Curves 927 A Figure 15 18 Section 15 1 Homeworklib




Solved Example 11 Sketch The Level Curves Of The Function Chegg Com




Matlab How Can I Get The Expression Of The Level Curves Of A Function Stack Overflow




Math 27 Winter 12 Assignment 2 1 Sketch The Level Curves Of



Www Math Uci Edu Remote Teaching Lecture Notes Of Hamed Math 2d lecture notes Lecture note 14 1 Pdf



Hgm4 14 Review 71 Gradients Etc Pg Query



Www Usna Edu Users Math Uhan Sm223 Lessons 12 level curves Pdf



Problem On Gradient Directional Derivative And Level Curves Leading Lesson



0 3 Visualizing Functions Of Several Variables



Answered Display The Values Of The Function In Bartleby



Level Sets Ximera




Use The Level Curves Of The Function To Determine If Each Partial Derivative At The Point P Is Positive Negative Or Zero Mathematics Stack Exchange




13 1 Functions Of Several Variables Mathematics Libretexts




Oneclass Find The Domain And Range And Describe The Level Curves For The Function F X Y F X Y V4



Http Www Math Drexel Edu Classes Calculus Resources Math0hw Homework13 1 Ans Pdf




Gate Ese Level Curves And Surface Of A Function In Hindi Offered By Unacademy




Level Curves Mit 18 02sc Multivariable Calculus Fall 10 Youtube




Level Sets Math Insight



How Do You Sketch Level Curves Of Multivariable Functions Vector Calculus 1 Youtube




How To Sketch Level Curves Youtube



Calculus Iii Functions Of Several Variables




Draw The Level Curve Of The Function F X Y X Y Containing The Point 3 3 Study Com




Calculus Iii Functions Of Several Variables



13 1



Http Www Personal Psu Edu Sxj937 Math111 Lecture 11 Pdf



0 3 Visualizing Functions Of Several Variables




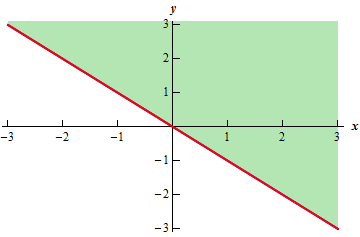
Describe The Level Curves Of The Function Z 8 2x 7y Chegg Com



1
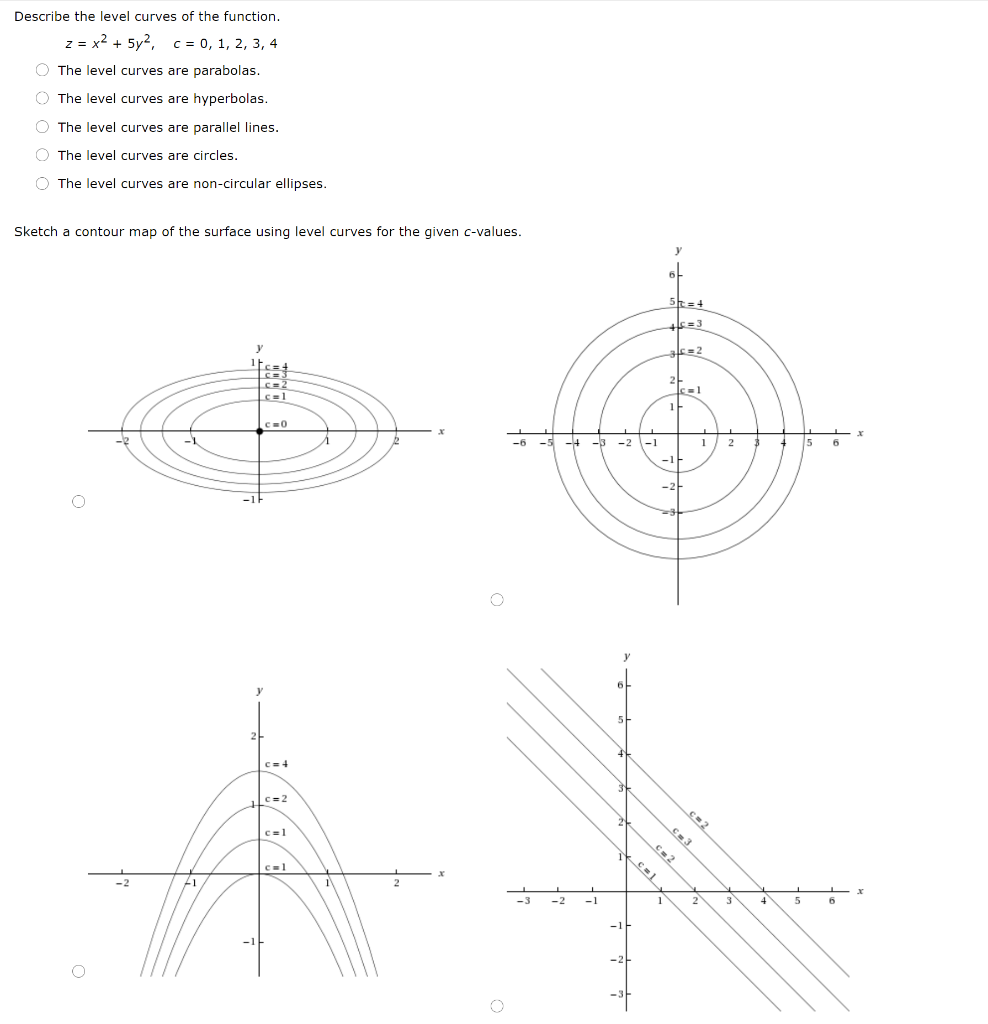



Describe The Level Curves Of The Function Z X2 Chegg Com



13 1



Solved The Figure Shows Level Curves Of A Functio




Calculus Iii Functions Of Several Variables



Answered Sketch The Level Curves Of The Function Bartleby



Www3 Nd Edu Taylor Math550 Images Currentexamsolutions Exam2f16 Pdf




Level Curves Curves Level Stvincent Glogster Edu Interactive Multimedia Posters



Www Jstor Org Stable




How Do You Sketch Level Curves Of Multivariable Functions Krista King Math Online Math Tutor




Calculus Iii Functions Of Several Variables




Level Curves




The Field Of The Condenser And The Level Curves Of The Function U For Download Scientific Diagram



Relief Functions And Level Curves




Level Curves And Implicit Differentiation Studocu




Get Answer Figure 18 61 Shows Level Curves Of The Function F X Y A Transtutors




Level Set Wikipedia



Mysite Science Uottawa Ca ionne Teaching Help Centre Level Curve Pdf




Finding A Function With Level Curves Mathematics Stack Exchange




Level Curves Example 1



Solved Sketch Several Level Curves Of The Function F X Y E X Y




Math 2110 Section 13 1 Level Curves And Level Surfaces Youtube




Level Curves




Sketch The Level Curves Of The Function G X Y Chegg Com



1




Level Set Examples Math Insight




Level Curves



Level Curves




Level Curves For The Riemann Zeta Function Maths Paper Graphic Zeta




Lesson 15 Gradients And Level Curves




Note On The Curvature Of Orthogonal Trajectories Of Level Curves Of Green S Function Pnas




Describe The Level Curves Of The Function Z X2 Chegg Com




Level Sets Math Insight




Level Sets Math Insight



Vb Helper Howto Draw Contour Plots Level Curves For A Function With Known Derivatives



Relief Functions And Level Curves




Level Set Wikipedia



8 Calculus Of Several Variables Functions Of Several Variables Ppt Download




A Find The Function S Domain B Find The Function S Range C Describe The Function S Level Curves D Find The Boundary Of The Function S Domain E Determine If The Domain Is An Open
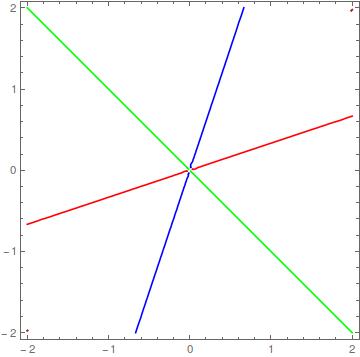



Find Two Level Curves Of The Function F X Y X Y X Y X Y And Sketch Them Socratic




012 Sketching Level Curves Of Multivariable Functions Pdf Docer Com Ar
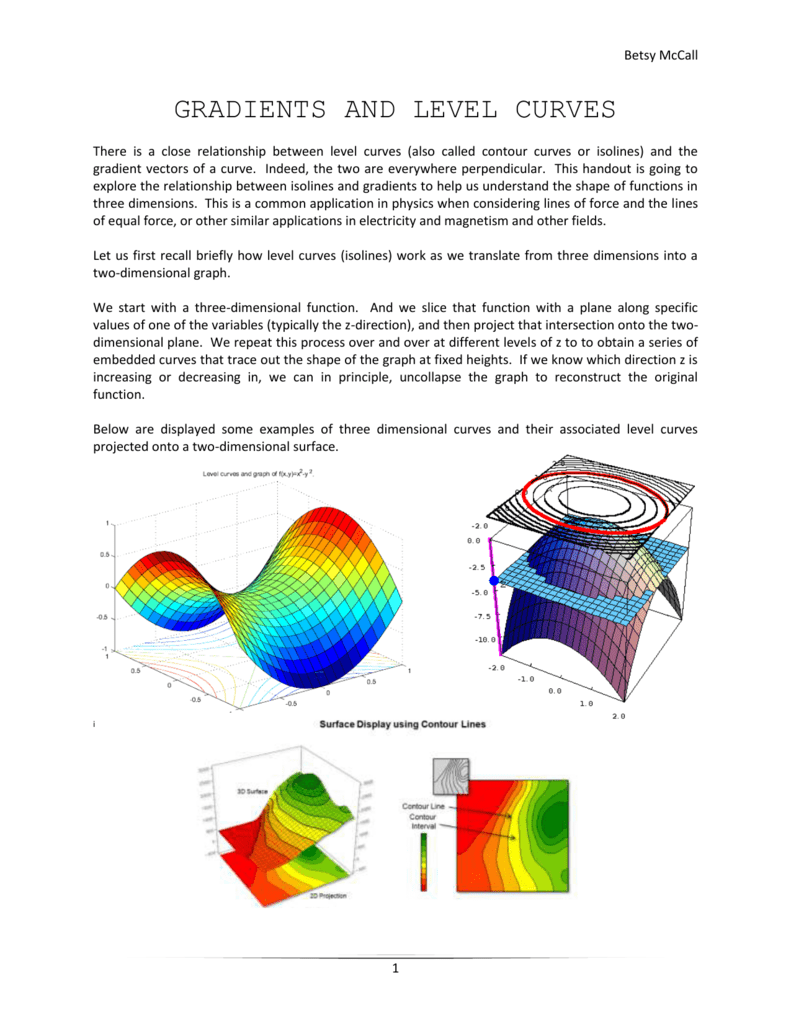



Gradients Level Curves



Users Math Msu Edu Users Bellro Lb2sp13 S4 Pdf
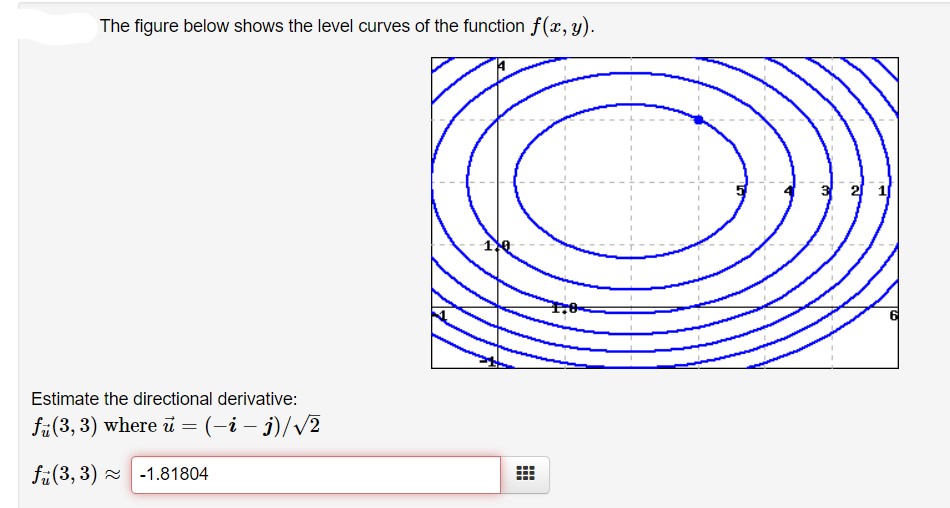



Answered The Figure Below Shows The Level Curves Bartleby




Calculus 11 1 Functions Of Several Variables Flashcards Quizlet



Http Math Wustl Edu Beheshti 14 1 Sol Pdf



Http Www Math Harvard Edu Knill Teaching Summer18 Handouts Week2 Pdf



0 件のコメント:
コメントを投稿